Свойства аффинного преобразования

1. Образом параллельных прямых являются параллельные прямые.

Доказательство от противного. Предположим, что образом параллельных прямых l и m являются пересекающиеся в точке А" прямые l" и m"(рис.8). В силу взаимной однозначности преобразования точка имеет прообраз, который обозначим А. Но так как А"єl", то Аєl. Аналогично Аєm. Это противоречит параллельности прямых l и m.

2. При аффинном преобразовании сохраняется отношение двух отрезков, расположенных на одной прямой: (рис.9)

В самом деле, по определению аффинного преобразования:

3. При аффинном преобразовании сохраняется отношение параллельных отрезков.

Дано: АВ||СD. По свойству 2 будет также А"В"||С"D"(рис.10)

Надо доказать:

Для доказательства проведем АС, затем DL||AC. Построим также А"С" и D"L"||A"C". По свойству 2 прямая DL переходит в D"L" и значит, . Теперь по определению: . Но AL=CD, A"L"=C"L", поэтому отсюда сразу получается требуемое.

4. При аффинном преобразовании угол и отношение произвольных отрезков, вообще говоря, не сохраняются, так как любой треугольник можно перевести в любой другой. Поэтому высота и биссектриса треугольника преобразуются обычно в другие линии, медиана же переходит в медиану, так как середина отрезка переходит в середину.

5. При аффинном преобразовании параллелограмм переходит в параллелограмм, трапеция в трапецию.

Эквивалентные фигуры

Аналогично понятию равенства и подобия фигур вводится понятие их аффинной эквивалентности.

Фигура F1 называется аффинно эквивалентной фигуре F2, если F1 можно аффинным преобразованием перевести в F2.

Корректность этого определения вытекает из того, что аффинные преобразования образуют группу и, следовательно, введенная здесь аффинная эквивалентность обладает транзитивностью, рефлексивностью, симметричностью.

Отметим некоторые классы аффинно эквивалентных фигур.

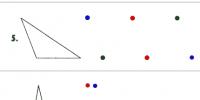
1). Все треугольники аффинно эквивалентны (следует из основной теоремы).

2). Все параллелограммы аффинно эквивалентны.

3). Для аффинной эквивалентности трапеций необходимо и достаточно, чтобы их основания были пропорциональны.

Перспективно-аффинное соответствие двух плоскостей

Предположим, что две плоскости w и w" пересекаются по линии хх (черт. 1). Зададим какую-нибудь прямую l, пересекающую обе плоскости. Отметим на плоскости w произвольную точку А и спроектируем ее на плоскость w", проводя через А прямую, параллельную l. Пусть проектирующая прямая пересечет плоскость w" в точке А". Точку А" можно рассматривать как проекцию точки А на плоскость w". Такая проекция называется параллельной и определяется заданием прямой l.

Из самого построения проекции А" точки А видно, что в свою очередь точку А можно рассматривать как проекцию точки А" на плоскость w. Таким образом, параллельная проекция представляет собой аппарат, имеющий совершенно одинаковое значение по отношению к обеим плоскостям w и w". Она относит каждой точке (А) первой плоскости вполне определенную точку (А") второй, и обратно. Мы получаем попарное соответствие точек плоскостей w и w". Это соответствие является взаимно однозначным, т. е. каждой точке одной плоскости соответствует единственная точка второй, и обратно.

Соответствие плоскостей w и w", установленное с помощью параллельной проекции, называется перспективно- аффинным или родственным.

Если рассматривают процесс перехода от одной из данных плоскостей (например, w) к другой плоскости (w"), при котором каждая точка (А) одной плоскости (w) переходит в соответствующую точку (А") другой плоскости (w"), как односторонний, то его называют преобразованием плоскости (w) в плоскость (w")- В этом случае точку А называют прообразом, а точку А" - ее образом.

Проектируя параллельно плоскость w на плоскость w" , производим перспективно-аффинное преобразование плоскости w в плоскость w" .

Можно также совокупность всех точек плоскости w называть полем точек w и говорить о преобразовании поля точек w в поле точек w".

Поставим себе задачу изучить свойства перспективно-аффинного соответствия плоскостей.

Займемся, прежде всего, вопросом о двойных, или неподвижных, точках нашего соответствия, т. е. о таких точках, которые совпадают со своими соответственными точками. Так как каждая двойная точка должна принадлежать как одной, так и другой плоскости, то они должны лежать на линии пересечения хх плоскостей w и w". С другой стороны, очевидно, что каждая точка прямой хх есть двойная, так как она сама себе соответствует. Прямая называется осью соответствия. Согласно предыдущему ось соответствия может быть определена как геометрическое место двойных точек.

Таким образом, прямой линии на одной плоскости соответствует прямая же линия на другой. Это свойство перспективно-аффинного соответствия называют коллинеарностью. В силу самого определения параллельной проекции фигуры как геометрического места проекций всех точек этой фигуры каждой точке, лежащей на прямой, всегда соответствует точка, лежащая на соответственной прямой. Поэтому взаимопринадлежность точки и прямой на одной плоскости влечет за собой взаимопринадлежность соответственных элементов на второй.

2. Следующее свойство перспективно-аффинного соответствия касается так называемого простого отношения трех точек прямой.

Рассмотрим три точки А, В, С, лежащие на одной прямой (черт 1). Простое отношение точек А, В, С определяется формулой:

геометрический преобразование аффинный соответствие

В этой формуле точки А и В считаются основными (или базисными), а точка С- делящей. Простое отношение (ABC) представляет собой отношение длин тех отрезков, которые делящая точка образует с основными. Если точка С лежит вне отрезка А В, то оба отрезка АС и ВС одинаково направлены, и поэтому в этом случае простое отношение (ABC) положительно. В случае, когда делящая точка С находится между А и В, простое отношение (ABC) отрицательно.

На чертеже 1 видно, что точкам А,В, С плоскости w соответствуют точки А", В", С" плоскости w". Так как проектирующие прямые АА", ВВ", СС" параллельны, то будем иметь:

или (ABC) = (А"В"С").

Мы приходим к выводу, что в перспективно-аффинном соответствии простое отношение трех точек прямой одной плоскости всегда равно простому отношению трех соответственных точек другой.

3. Прежде чем перейти к рассмотрению дальнейших свойств перспективно-аффинного соответствия, остановимся на вопросе о возможном расположении соответственных плоскостей w и w" в пространстве.

До сих пор мы предполагали эти плоскости несовпадающими и пересекающимися по линии хх с той целью, чтобы посредством параллельного проектирования установить рассмотренное выше перспективно-аффинное соответствие. После того как такое соответствие установлено, можно было бы привести обе плоскости в совпадение, вращая какую-либо одну из них вокруг оси хх. При этом все геометрические образы, находящиеся в той и другой плоскости, не подвергаются никакому изменению. Следовательно, как в любой момент вращения плоскости, так и при ее совмещении со второй плоскостью установленное ранее перспективно-аффинное соответствие не нарушается.

Прямые, соединяющие соответственные точки, как АА", ВВ", СС",…, остаются параллельными при любом положении вращающейся плоскости, а также и после ее совмещения с неподвижной плоскостью. Это видно из того, что каждые две из упомянутых прямых (например, АА" и ВВ") всегда лежат в одной плоскости, определяемой парой пересекающихся прямых (АВ и А"В"), и отсекают на сторонах угла пропорциональные отрезки, так как (АВХ) = (А"В"Х). При совмещении плоскостей w и w" проектирующие прямые (АА", ВВ",...) окажутся лежащими в плоскости, образовавшейся из двух совпавших плоскостей w и w" (черт. 2).

Для нас особенно интересен случай совмещенного положения плоскостей так как в этом случае мы можем пользоваться плоским чертежом, изображающим установленное соответствие без искажения.

В случае совмещения каждую точку (двойной) плоскости можно рассматривать как принадлежащую плоскости w или w" и обозначать ее в зависимости от этого большой буквой без штриха или со штрихом. Таким образом, мы имеем преобразование плоскости в себя, причем ее начальное состояние (плоскость до преобразования) обозначается буквой w, а новое состояние (плоскость после преобразования) - буквой w".

Заметим, что после совмещения плоскостей ось соответствия хх перестает быть линией пересечения данных плоскостей, но за ней сохраняется второе определение как геометрического места двойных, или неподвижных, точек.

4. Теперь мы могли бы отказаться от пространственного аппарата (параллельной проекции), послужившего нам для установления перспективно-аффинного соответствия двух плоскостей, и определить последнее для двойной плоскости, не выходя в пространство. С этой целью докажем следующее предположение: Перспективно-аффинное преобразование плоскости в себя вполне определяется осью (хх) и парой соответственных точек (А, А").

Доказательство. Пусть даны ось хх и пара соответственных точек (АА") перспективно-аффинного преобразования (черт. 3). Докажем, что для любой точки В плоскости можно построить вполне определенную и единственную соответственную точку В".

Проведем прямую АВ. Пусть X -точка ее пересечения с осью хх. Так как точка X сама себе соответствует (как лежащая на оси), то прямой АХ соответствует прямая А"X. Наконец, точка В" должна лежать на прямой А"Х и проектирующей прямой ВВ", параллельной А А". Это позволяет построить искомую точку В". Таким образом, данных оказалось достаточно, и соответственная точка В" представляет единственное решение.

Заметим, что перспективно-аффинное соответствие будет действительно реализовано, так как указанная конструкция не может привести к противоречию. Это легко проверить, сведя построение к аппарату параллельной проекции.

В самом деле, если перегнем чертеж 3 по линии хх так, чтобы плоскости w и w" образовали двугранный угол, то все проектирующие прямые (прямые, соединяющие соответственные точки, например ВВ") окажутся параллельными прямой АА" (в силу пропорциональности отрезков). Следовательно, построенное нами соответствие можно рассматривать как результат параллельной проекции.

Примечание. Если бы на чертеже 3 мы отнесли точку В к плоскости w", обозначив ее через С", то построение соответственной точки привело бы нас к точке С, которая, как видно из чертежа 3, не всегда совпадает с В". Можно доказать, что необходимое и достаточное условие такого совпадения, т. е. независимости перспективно-аффинного соответствия от того, отнесена ли точка к той или другой плоскости, заключается в делении отрезка А А" пополам в точке пересечения его с осью хх.

Следовательно, в этом случае соответствие является косой или прямой симметрией (относительно оси хх).

5. В дальнейшем исследовании перспективно-аффинного соответствия мы будем опираться на установленные выше свойства: 1) коллинеарность и 2) равенство простых отношений троек соответственных точек.

Заметим, что в перспективно-аффинных преобразованиях эти свойства выражают неизменность, или инвариантность, понятия прямой линии и понятия простого отношения трех точек прямой.

Из этих свойств можно вывести целый ряд других «инвариантов» перспективно-аффинного преобразования, которые, таким образом, уже не являются независимыми. Докажем прежде всего инвариантность параллелизма прямых. Предположим, что на плоскости w имеем две прямые а и b, которым на плоскости w" соответствуют прямые а" и b". Предположим, что прямые а и b параллельны (а || b). Докажем, что а "|| b". Применим доказательство «от противного». Предположим, что прямые а" и b" пересекаются, и обозначим точку пересечения буквой М" (черт. 4). Тогда в силу взаимно однозначного соответствия плоскостей w и w" точке М" плоскости w" соответствует точка М на плоскости w. Точка М должна принадлежать как прямой а, так и прямой b. Следовательно, М есть точка пересечения прямых а и b. Таким образом, приходим к противоречию. Предположение, что прямые а" и b" пересекаются, невозможно. Поэтому а" || b".

Таким образом, параллелизм прямых есть инвариантное свойство перспективно-аффинного преобразования.

Соединим В с D и проведем через С прямую СF || DВ. На плоскости w" прямой СF будет соответствовать прямая С"F" D"В" (в силу инвариантности параллелизма) и, следовательно, точке F будет соответствовать точка F". Зная, что простое отношение трех точек инвариантно, можем написать:

Таким образом, приходим к равенству:

Последнее показывает, что отношение двух параллельных отрезков есть инвариант перспективно-аффинного соответствия.

Если отрезки АВ и СD лежат на одной прямой (черт. 6), то их отношение также инвариантно в перспективно-аффинном соответствии. В самом деле, пусть РQ-произвольный отрезок, параллельный прямой АВ. Тогда имеем:

6. Переходим к рассмотрению площадей соответственных фигур. Докажем следующую лемму: Расстояния двух соответственных точек (А, А") до оси соответствия (хх) находятся в постоянном отношении, не зависящем от выбора пары соответственных точек. Доказательство. Предположим, что точкам А и В соответствуют точки А" и В" (черт. 7). Опуская из этих точек перпендикуляры на ось хх, получим расстояния их до оси. Расстояния будем всегда рассматривать положительными независимо от направления перпендикуляров.

Можем написать:

Но как видно из чертежа:

Полученное равенство и доказывает формулированную выше лемму.

Обозначим постоянное отношение расстояний соответственных точек через к. Докажем следующую теорему.

Отношение площадей двух соответственных треугольников постоянно и равно к.

Доказательство теоремы распадается на следующие случаи:

1. Треугольники имеют общую сторону на оси хх.

Такие треугольники представлены на чертеже 8. Отношение их площадей выразится следующим образом:

2. Треугольники имеют общую вершину на оси хх.

Таковы два треугольника на чертеже 9. Соответственные стороны ВС и В"С" этих треугольников должны пересекаться на оси хх (в точке X). Рассматриваемый случай сводится к предыдущему. В самом деле, на основании предыдущего можно написать:

Поэтому будем иметь:

3. Общий случай двух соответственных треугольников.

Пусть на чертеже 10 имеем два соответственных треугольника ABC и А"В"С". Рассмотрим один из этих треугольников, например ABC. Площадь этого треугольника можно представить следующим образом:

Все треугольники правой части этого равенства относятся к рассмотренным уже двум случаям, поэтому, применяя к ним доказанную теорему, можем переписать найденное выше равенство так:

Следовательно,

7. Выведенное нами свойство площадей двух соответственных треугольников легко распространить на случай соответственных многоугольников. В самом деле, каждый многоугольник может быть разбит на несколько треугольников, причем площадь многоугольника выразится суммой площадей составляющих его треугольников.

Для соответственного многоугольника получим аналогичное разбиение на треугольники. Если площади двух соответственных многоугольников обозначим буквами S и S", а площади двух соответственных составляющих треугольников -- буквами, то можем написать:

Так как, кроме того, для площадей соответственных треугольников имеем:

Таким образом, получаем:

Наконец, можно обобщить теорему об отношении площадей на случай двух площадей, ограниченных соответственными кривыми произвольного вида.

Обозначим площади, ограниченные двумя соответственными кривыми, через и. Впишем многоугольник в кривую, ограничивающую площадь, и обозначим площадь этого многоугольника буквой S. Будем увеличивать число сторон вписанного многоугольника до бесконечности при условии, что каждая сторона его стремится к нулю, тогда получим:

Для площади будем иметь аналогичный процесс: ,

где через S" обозначена площадь многоугольника, соответственного многоугольнику S. Так как в течение всего процесса (изменения многоугольников), согласно доказанной выше теореме, должны иметь:

то переход к пределу дает =k.

Следовательно,

Полученное свойство может быть представлено как инвариант перспективно-аффинного соответствия.

В самом деле, обозначим через и площади, ограниченные двумя кривыми произвольного вида, а через " и " - площади, ограниченные соответственными кривыми, тогда, по доказанному, будем иметь:

или, переставляя средние члены пропорции:

что может быть выражено следующими словами: отношение двух каких-либо площадей не изменяется (является инвариантом) в перспективно-аффинном соответствии.

Общее аффинное соответствие

Перспективно-аффинное соответствие двух плоскостей может быть получено с помощью параллельной проекции.

Рассмотрим теперь соответствие двух плоскостей, образованное многократным применением параллельного проектирования. Так, на чертеже 11 плоскость w проектируется параллельно прямой l на плоскость w". Эта плоскость проектируется параллельно прямой l" на плоскость w". Наконец, последняя проектируется параллельно прямой l" на плоскость w"". Таким образом, между плоскостями w и w""устанавливается соответствие, в котором точкам A,B,C первой плоскости соответствуют точки А"", В"", С" второй. Нетрудно убедиться в том, что это соответствие может не быть параллельной проекцией, но в то же время обладает инвариантными свойствами перспективно-аффинного соответствия. В самом деле, соответствие плоскостей w и w"" является цепью последовательных параллельных проектирований. Так как каждое такое проектирование сохраняет коллинеарность и простое отношение трех точек, то теми же свойствами должно, очевидно, обладать и результирующее соответствие плоскостей w и w""".

То же самое можно сказать и об остальных инвариантных свойствах, рассмотренных в случае перспективно-аффинного соответствия, которое оказывается, таким образом, лишь тем частным случаем, когда прямые, соединяющие соответственные точки, параллельны между собой:

По этой именно причине такое соответствие называется перспективно- аффинным.

Соответствие же плоскостей w и w""" называется аффинным. Мы пришли к этому понятию, воспользовавшись цепью перспективно-аффинных преобразований (или параллельных проекций). Если каждое из них обозначим буквами Р, Р",Р" а результирующее преобразование -- буквой А, можем представить аффинное преобразование А следующей символической формулой:

А = Р * Р" * Р",

в которой правая часть представляет собой «произведение» перспективно-аффинных преобразований, т. е. результат их последовательного применения.

Те же рассуждения можно было бы провести, не выходя из одной плоскости, для чего достаточно рассматривать цепь перспективно-аффинных преобразований плоскости в себя. Каждое из преобразований может быть задано осью и парой соответственных точек. Так, например, на чертеже 12 первое преобразование Р задано осью хх и парой (А, А"); второе Р" -- осью и парой (А", А"); третье Р" -- осью х"х" и парой (А"" А""). В результирующем преобразовании А точке А соответствует точка А"". На том же чертеже показано построение точки В"", соответственной точке В.

Изложенное показывает, что преобразования, полученные при помощи цепи параллельных проекций (или перспективно-аффинных преобразований), обладают свойствами коллинеарности и сохранения простого отношения трех точек.

УДК 004.932

Кудрина М.А., Мурзин А.В.

ФГБОУ ВПО "Самарский государственный аэрокосмический университет им. ак. С.П. Королева (национальный исследовательский университет)", Самара, Россия

АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В КОМПЬЮТЕРНОЙ ГРАФИКЕ

Одной из типовых задач, которую приходится решать средствами растровой изобразительной графики, является преобразование как всего изображения в целом, так и его отдельных фрагментов, как то: перемещение, поворот вокруг заданного центра, изменение линейных размеров и т.п.

Данная задача решается использованием аффинных преобразований (affine transformations) .

Аффинные преобразования могут быть очень полезны в следующих ситуациях:

1. Для составления плоского изображения или трехмерной сцены путем компоновки из однотипных элементов, с помощью их копирования, преобразования и перемещения в различные места изображения. Например, для создания симметричных объектов, таких, как снежинка. Можно разработать один мотив и затем составить изображение всего объекта путем отражений, поворотов и перемещений данного мотива.

2. Для просмотра трехмерных объектов с различных точек зрения. В этом случае можно зафиксировать положение камеры и поворачивать сцену или наоборот, сцену оставить неподвижной и передвигать вокруг нее камеру. Подобные манипуляции могут быть осуществлены с помощью трехмерных аффинных преобразований.

3. Для проецирования трехмерных объектов на плоскость и отображения сцены в окне. Так, например, для аксонометрического проецирования используется последовательность двух поворотов плоскости проецирования, а для отображения в окне - совокупность масштабирования и перемещения.

Аффинные преобразования на плоскости в общем виде описываются следующими формулами:

J X = Ax + By + C, . Программа позволяет автоматизировать процесс составления тестовых задач.

ЛИТЕРАТУРА

1. Порев В. Н. Компьютерная графика. - СПб.: БХВ-Петербург, 2002. - 432 с. : ил.

2. Хилл Ф. Open GL. Программирование компьютерной графики. Для профессионалов. - СПб.:Питер,

2002. - 1088с.:ил. ISBN 5-318-00219-6

3. Кудрина М.А., Кудрин К.А., Вытягов А.А., Ионов Д.О. Разработка системы дистанционного обучения для курса "Компьютерная графика" с помощью Moodle: Труды международного симпозиума Надежность и качество. 2010. Т. I. С. 165.

4. Кудрина М.А., Кудрин К.А., Дегтярева О.А. Аттестационный педагогический измерительный материал по курсу "Компьютерная графика"// Надежность и качество 2008. Труды межд. симпозиума. Пенза, 2008, С. 162-163.

5. Кудрина М.А. Использование аттестационно-педагогических измерительных материалов по курсу

"Компьютерная графика" в учебном процессе"//Образование - инвестиции в успех: Материалы науч.-

Тема этого выпуска задание аффинного преобразования в матричной форме. Эта тема, по сути, является обобщением всего, что было сказано ранее.

Определение. Преобразование плоскости называется аффинным , если

• оно взаимно однозначно;
• образом любой прямой является прямая.

Преобразование называется взаимно однозначным , если

• разные точки переходят в разные;
• в каждую точку переходит какая-то точка.

Однородные координаты

Если рассмотреть параллельный перенос, то оказывается, что для его задания матрицы 2x2 уже недостаточно. Но его можно задать с помощью матрицы размера 3x3. Появляется вопрос, откуда взять третью координату у двумерной точки?

Определение. Однородные координаты - координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у) является тройка чисел (x", y", h) , где х = х" / h, у = y"/h, а h - некоторое вещественное число (случай, когда h = 0 является особым).

Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1 , 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1) . Предлагается взять набор (x, y, 1) , который будет описывать все точки плоскости.

Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах.

Сжатие/растяжение

Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y ) -> (a x * x , a y * y ) . Матрица преобразования запишется следующим образом:

[ a x 0 0 ]

Где a x – растяжение по оси x ,

a y – растяжение по оси y .

Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.

Поворот

Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:

[ -sin(phi)cos(phi) 0]

Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).

Параллельный перенос

Исходный вектор (x, y ) переходит в (x + t x, y + t y ) . Матрица преобразования запишется следующим образом:

[ 1 0 0]

[ t x t y 1]

Отражение

Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:

[-10 0]

отражение относительно оси x

отражение относительно оси y

Общий вид аффинного преобразования

Матрица 3x3, последний столбец которой равен (0 0 1) T , задает аффинное преобразование плоскости:

[ * * 0]

[ * * 0]

[ * * 1]

По одному из свойств, аффинное преобразование можно записать в виде:

f (x ) = x * R + t ,

где R – обратимая матрица 2 x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:

[ R 1,1 R 1,2 0 ]

[ R 2,1 R 2,2 0 ]

[ t x t y 1 ]

Если умножить вектор-строку на эту матрицу получаем результат преобразования:

[ xy1 ] *[ R 1,1 R 1,2 0 ]

[ R 2,1 R 2,2 0 ]

[ t x t y 1 ]

[ x’y’1 ]+[ t x t y 1 ]

При этом [ x ’ y ’ ]= R *[ x y ]

Прим. Любопытный читатель уже задал себе вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади всех фигур изменяются в | R|. (Можно строго доказать это с точки зрения математики, но здесь этот факт приводится без доказательства.)

Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R , и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R 1,1, R 1,2 ), вектор (0, 1) переходит в (R 2,1, R 2,2 ). Новый базис это строки матрицы R .

Пример.

При отражении относительно оси y , базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0) . Т.о. матрица R будет выглядеть следующим образом:

Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:

Выше приведены базовые сведения о таком мощном инструменте, как аффинное преобразование. Остается много вопросов: какой подкласс аффинных преобразований сохраняет углы между прямыми? Как можно представить аффинное преобразование в виде композиции нескольких подклассов? Как задавать более сложные преобразования, например, осевая симметрия относительно произвольной прямой?

Ответы на эти вопросы и более детальное рассмотрение аффинного преобразования будут приведены отдельно, в качестве раздела курса теоретической геометрии.

Остановимся на практической реализации аффинного преобразования в виде демонстрационной программы. К возможностям приложения, демонстрирующего поворот плоскости мышью, добавляются функции параллельного переноса при нажатой клавише CTRL .

Т.к. эта статья является завершающей в данном разделе, код демонстрационного приложения должен быть соответствующим. Давайте попробуем разобраться, какие блоки нужны в графическом приложении, параллельно рассматривая, как они реализованы в данной программе:

• блок, в котором происходит создание окна и обрабатываются сообщения операционной системы, реализован в файл emain . cpp
• графический движок, выполняющий отрисовку изображения, класс Engine
• прослойка, необходимая для преобразования логических координат в оконные и обратно, класс Viewport
• объект, отвечающий за реакцию на действия пользователя, класс Action

В приведенном примере реализованы эти функциональные блоки, с подробными комментариями.

Глава I.Понятие о геометрическом преобразовании

1.1 Что такое геометрическое преобразование?

Осевая симметрия, центральная симметрия, поворот, параллельный перенос, гомотетия имеют то общее, что все они „преобразуют" каждую фигуру Fв некоторую новую фигуру F1. Поэтому их называют геометрическими преобразованиями.

Вообще, геометрическим преобразованием называют всякое правило, позволяющее для каждой точки А на плоскости указать новую точку A", в которую переводится точка А рассматриваемым преобразованием. Если на плоскости задана какая-либо фигура F, то множество всех точек, в которые переходят тонки фигуры Fпри рассматриваемом преобразовании, представляет собой новую фигуру F., В этом случае говорят, что F" получается из F при помощи рассматриваемого преобразования.

Пример. Симметрия относительно прямой l является геометрическим преобразованием. Правило, позволяющее по точке A найти соответствующую ей точку А", в этом случае заключается в следующем: из точки А опускается перпендикуляр АР на прямую lи на его продолжении за точку Р откладывается отрезок РА"=АР.

Сложение геометрических преобразований

Предположим, что мы рассматриваем два геометрических преобразования, одно из которых называем „первым", а другое - „вторым". Возьмем на плоскости произвольную точку А и обозначим через А" ту точку, в которую переходит А при первом преобразовании. В свою очередь точка А" переводится вторым преобразованием в некоторую новую точку А". Иначе говоря, точка А" получается из точки А при помощи последовательного применения двух преобразований - сначала первого, а затем второго.

Результат последовательного выполнения взятых двух преобразований также представляет собой геометрическое преобразование: оно переводит точку А в точку А". Это „результирующее" преобразование называется суммой первого и второго рассмотренных преобразований.

Пусть на плоскости задана какая-либо фигура F. Первое преобразование переводит ее в некоторую фигуру F" . Вторым преобразованием эта фигура F" переводится в некоторую новую фигуру F"". Сумма же первого и второго преобразований сразу переводит фигуру Fв фигуру F".

Пример. Пусть первое преобразование представляет собой симметрию относительно точки О1 а второе преобразование - симметрию относительно другой точки О2. Найдем сумму этих двух преобразований.

Пусть А - произвольная точка плоскости. Предположим сначала, что точка A не лежит на прямой O1O2. Обозначим через А" точку, симметричную точке А относительно О1, а через A" - точку, симметричную точке A" относительно О2 . Так как О1O2 - средняя линия треугольника АА"А"" то отрезок АА" параллелен отрезку О1O2 и имеет вдвое большую длину. Направление от точки А к точке А" совпадает с направлением от точки

О1 к точке О2. Обозначим теперь через МNтакой вектор, что отрезки MNи O1 O2 параллельны, отрезок МNв два раза длиннее отрезка O1О2 и лучи МNи O1O2 имеют одно и то же направление. Тогда АА" = МN, т. е. точка А" получается из точки А параллельным переносом на вектор МN.

То же справедливо и для точки, лежащей на прямой O1О2.

Окончательно мы получаем: сумма симметрии относительно точки O1 и симметрии относительно точки O2 представляет собой параллельный, перенос.

1.2 Движения

Осевая симметрия, поворот (в частности, центральная симметрия) и параллельный перенос имеют то общее, что каждое из этих преобразований переводит любую фигуру F на плоскости в равную ей фигуру F" . Преобразования, обладающие этим свойством, называются движениями. Гомотетия представляет собой пример преобразования, не являющегося движением. Действительно, каждое движение переводит любую фигуру в равную ей фигуру, т. е. изменяет лишь положение фигур на плоскости; гомотетия же изменяет и размеры фигур.

Роль движений в геометрии

Движения играют в геометрии чрезвычайно важную роль. Они не изменяют ни формы, ни размеров фигур, меняя лишь расположение фигуры. Но фигуры, отличающиеся лишь своим расположением на плоскости, с точки зрения геометрии совершенно одинаковы. Именно поэтому их и называют в геометрии «равными фигурами». Ни одно свойство геометрической фигуры не отличается от соответствующего свойства равной ей фигуры. Так, например, равные треугольники имеют не только одинаковые стороны, но и одинаковые углы, медианы, биссектрисы, площади, радиусы вписанной и описанной окружностей и так далее.

На уроках геометрии мы всегда считали равные фигуры (т. е. такие, которые можно совместить при помощи движения) одинаковыми или неразличимыми. Такие фигуры часто принимают за одну и ту же фигуру. Именно поэтому мы можем сказать, что, например, задача построения треугольника по двум сторонам а, bи заключенному между ними углу С имеет только одно решение. На самом деле, конечно, треугольников, имеющих данные стороны а и b и заключенный между ними угол С данной величины, можно найти бесконечно много. Однако все эти треугольники одинаковы, равны, поэтому их можно принять за «один» треугольник.

Таким образом, геометрия изучает те свойства фигур, которые одинаковы у равных фигур. Такие свойства можно назвать «геометрическими свойствами». Другими словами: геометрия изучает свойства фигур, не зависящие от их расположения. Но фигуры, отличающиеся только расположением (равные фигуры), - это те, которые можно совместить с помощью движения. Поэтому мы приходим к следующему определению предмета геометрии; геометрия изучает те свойства фигур, которые сохраняются при движениях.

Движения в геометрии и физике

Итак, понятие движения играет в геометрии первостепенную роль. Движения («наложения») использовались в VI классе для определения равных фигур, для доказательства признаков равенства треугольников; понятие движения, как мы видели выше, позволяет также дать описание предмета геометрии.

Между тем в определениях понятия равенства фигур и понятия движения имеется пробел. В самом деле, равные фигуры определялись (в VI классе) как такие фигуры, которые могут быть совмещены наложением (т. е. движением). Движения же были определены выше как такие преобразования, которые переводят два многоугольника F1 и Fтаковы, что существует многоугольник F", гомотетичный Fи равный F1 , то углы многоугольника Fсоответственно равны углам многоугольника F" и стороны многоугольника Fсоответственно, пропорциональны сторонам многоугольника F". Но у многоугольника F те же самые углы и стороны, что и у равного ему многоугольника F1. Следовательно, многоугольники F1и F подобны в том смысле, в каком это понималось в курсе геометрии VIII класса.

Обратно, пусть многоугольники F1 и F таковы, что их углы соответственно равны и стороны соответственно пропорциональны. Отношение сторон многоугольника F1 к соответствующим сторонам многоугольника Fобозначим через k. Далее, обозначим через F" многоугольник, получающийся из Fгомотетией с коэффициентом k (и каким угодно центром гомотетии. В таком случае в силу теоремы многоугольники F" и F1 будут иметь соответственно равные стороны и углы, т. е. эти многоугольники будут равны. Поэтому многоугольники F1 и Fбудут подобны и в смысле приведенного здесь определения подобия.

Глава II.Аффинные преобразования

2.1 Аффинные преобразования плоскости

Аффинным преобразованием α называется такое преобразование плоскости, которое всякую прямую переводит в прямую и сохраняет отношение, в котором точка делит отрезок.

На рис.1: L"= α(L), A"=α(A), B"=α(B), C"=α(C),

|

Преобразования - движение и подобие - являются частными случаями аффинных, так как в силу свойств движения и подобия для них выполнены все требования определения аффинных преобразований.

Приведем пример аффинного преобразования, не сводящегося к ранее рассмотренным. С этой целью сначала рассмотрим параллельное проектирование плоскости на плоскость.

Пусть даны плоскости: w и w1 прямая l(направление проектирования), не параллельная ни одной из этих плоскостей (рис.2). Точка Аєw называется проекцией точки А1єw1, если АА1||l , то прямая АА1 называется проектирующей прямой. Параллельное проектирование представляет собой отображение плоскости w1 на w.

Отметим следующие свойства параллельного проектирования.

1) Образом всякой прямой а1 является прямая.

В самом деле, прямые, проектирующие точки прямой а1, образуют плоскость (она проходит через а1 параллельно l), которая при пересечении с wдает образ прямой а1 – прямую а(рис.2).

2) Отношение, в котором точка делит отрезок, сохраняется, т.е.

(рис.2)

Сразу следует из теоремы о пересечении сторон угла параллельными прямыми.

Перейдем непосредственно к построению примера аффинного преобразования.

Возьмем два экземпляра плоскости w и один из них переместим в другое положение w1(рис.3). Новое положение какой-либо точки Аєwобозначим А1єw1. Теперь плоскость w1 спроектируем в каком-нибудь положении на w, проекцию точки А1 обозначим А".

Получилось преобразование плоскости w на себя, при котором

. В силу симметричных свойств параллельного проектирования для данного преобразования выполняются оба требования определенного аффинного преобразования, следовательно, построенное сейчас преобразование –перспективно- аффинное.

Ниже \(f\) обозначает аффинное преобразование, записываемое в декартовой системе координат \(O, \boldsymbol{e}_{1}, \boldsymbol{e}_{2}\) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1},\ y^{*}=a_{2}x+b_{2}y+c_{2}.\label{ref1}
$$
при условии
$$
\begin{vmatrix}
a_{1}& b_{1}\\
a_{2}& b_{2}
\end{vmatrix} \neq 0.\label{ref2}
$$

Рассмотрим на плоскости прямую линию с уравнением \(\boldsymbol{r}=\boldsymbol{r}_{0}+\boldsymbol{a}t\) и найдем ее образ при преобразовании \(f\). (Под образом прямой понимается множество образов ее точек.) Радиус-вектор образа \(M^{*}\) произвольной точки \(M\) можно вычислить так:
$$
\overrightarrow{OM^{*}}=\overrightarrow{Of(O)}+f\overrightarrow{(O)M^{*}}=\boldsymbol{c}+f(\boldsymbol{r}).\nonumber
$$

Здесь \(\boldsymbol{c}\) - постоянный вектор \(\overrightarrow{Of}(O)\), а \(\boldsymbol{r}\) - радиус-вектор точки \(M\). Согласно (11) §2 мы получаем
$$
\overrightarrow{OM^{*}}=\boldsymbol{c}+f(\boldsymbol{r}_{0})+f(\boldsymbol{a})t.\label{ref3}
$$
Так как \(f\) - аффинное преобразование и \(\boldsymbol{a} \neq \boldsymbol{0}\), то \(\boldsymbol{a}\) перейдет в вектор \(f(\boldsymbol{a}) \neq 0\), и уравнение \eqref{ref3} является уравнением прямой линии. Итак, образы всех точек прямой \(\boldsymbol{r}=\boldsymbol{r}_{0}+\boldsymbol{a}t\) лежат на прямой \eqref{ref3}.

Более того, преобразование \(f\) определяет взаимно однозначное отображение одной прямой на другую, так как при сделанном здесь выборе начальных точек и направляющих векторов точка \(M^{*}\) имеет на прямой \eqref{ref3} то же значение параметра \(t\), что и точка \(M\) на исходной прямой. Отсюда мы получаем первое утверждение.

Утверждение 1.

При аффинном преобразовании:

• прямая линия переходит в прямую линию;
• отрезок переходит в отрезок;
• параллельные прямые переходят в параллельные.

Доказательство.

Для доказательства второго утверждения достаточно заметить, что отрезок прямой состоит из таких точек, у которых значения параметра удовлетворяют неравенству вида \(t_{1} \leq t \leq t_{2}\) Третье утверждение следует из того, что при аффинном преобразовании коллинеар-ные векторы переходят в коллинеарные.

Утверждение 2.

При аффинном преобразовании отношение длин параллельных отрезков не изменяется.

Доказательство.

Пусть отрезки \(AB\) и \(CD\) параллельны. Это значит, что существует такое число \(\lambda\), что \(\overrightarrow{AB}=\lambda \overrightarrow{CD}\). Образы векторов \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) связаны той же зависимостью \(\overrightarrow{A^{*}B^{*}}=\lambda \overrightarrow{C^{*}D^{*}}\). Отсюда вытекает, что
$$
\frac{|\overrightarrow{AB}|}{|\overrightarrow{CD}|}=\frac{|\overrightarrow{A^{*}B^{*}}|}{|\overrightarrow{C^{*}D^{*}}|}=|\lambda|.\nonumber
$$

Следствие.

Если точка \(C\) делит отрезок \(AB\) в некотором отношении \(\lambda\), то ее образ \(C^{*}\) делит образ \(A^{*}B^{*}\) отрезка \(AB\) в том же отношении \(\lambda\).

Изменение площадей при аффинном преобразовании.

Для начала рассмотрим . Выберем общую декартову систему координат \(O, \boldsymbol{e}_{1}, \boldsymbol{e}_{2}\) и обозначим через \((p_{1}, p_{2})\) и \((q_{1}, q_{2})\) компоненты векторов \(\boldsymbol{p}\) и \(\boldsymbol{q}\), на которых он построен. Площадь параллелограмма мы можем вычислить, пользуясь :
$$
S_{\pm}=S_{\pm} (\boldsymbol{p}, \boldsymbol{q})=(p_{1}q_{2}-p_{2}q_{1}) S_{\pm} (\boldsymbol{e}_{1}, \boldsymbol{e}_{2}).\nonumber
$$

Пусть аффинное преобразование \(f\) записывается в выбранной системе координат формулами \eqref{ref1}. Из ранее доказанного следует, что векторы \(f(\boldsymbol{p})\) и \(f(\boldsymbol{q})\) имеют в базисе \(f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2})\) те же компоненты \((p_{1}, p_{2})\) и \((q_{1}, q_{2})\), что и векторы \(\boldsymbol{p}\) и \(\boldsymbol{q}\) в базисе \(\boldsymbol{e}_{1}, \boldsymbol{e}_{2}\). Образ параллелограмма построен на векторах \(f(\boldsymbol{p})\) и \(f(\boldsymbol{q})\), и площадь его равна
$$
S_{\pm}^{*}=S_{\pm} (f(\boldsymbol{p}), f(\boldsymbol{q}))=(p_{1}q_{2}-p_{2}q_{1}) S_{\pm} (f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2})).\nonumber
$$

Вычислим последний множитель. Как мы знаем из уже доказанного , координаты векторов \(f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2})\) равны соответственно \((a_{1}, a_{2})\) и \((b_{1}, b_{2})\). Поэтому \(S_{\pm} (f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2}))=(a_{1}b_{2}-a_{2}b_{1}) S_{\pm} (\boldsymbol{e}_{1}, \boldsymbol{e}_{2})\) и
$$
S_{\pm}^{*}=(p_{1}q_{2}-p_{2}q_{1})(a_{1}b_{2}-a_{2}b_{1}) S_{\pm} (\boldsymbol{e}_{1}, \boldsymbol{e}_{2}).\nonumber
$$
Отсюда мы видим, что
$$
\frac{S_{\pm}^{*}}{S_{\pm}}=\begin{vmatrix}
a_{1}& b_{1}\\
a_{2}& b_{2}
\end{vmatrix}.\label{ref4}
$$

Таким образом, отношение площади образа ориентированного параллелограмма к площади этого параллелограмма одинаково для всех параллелограммов и равно \(a_{1}b_{2}-a_{2}b_{1}\).

Отсюда следует, что данный детерминант не зависит от выбора системы координат, в которой записано преобразование, хотя он вычисляется по коэффициентам, зависящим от системы координат. Эта величина - инвариант, выражающий геометрическое свойство преобразования.

Из формулы \eqref{ref4} видно, что отношение площади образа неориентированного параллелограмма к его площади равно
$$
S^{*}/S=|a_{1}b_{2}-a_{2}b_{1}|.\label{ref5}
$$

Если \(a_{1}b_{2}-a_{2}b_{1} > 0\), то ориентации всех ориентированных параллелограммов сохраняются при преобразовании, а если \(a_{1}b_{2}-a_{2}b_{1} < 0\), то для каждого ориентированного параллелограмма ориентация образа противоположна его ориентации.

Займемся теперь площадями других фигур. Каждый треугольник может быть дополнен до параллелограмма, площадь которого равна удвоенной площади треугольника. Поэтому отношение площади образа треугольника к площади этого треугольника удовлетворяет равенству \eqref{ref5}.

Каждый многоугольник может быть разбит на треугольники. Следовательно, формула \eqref{ref5} справедлива и для произвольных многоугольников.

Мы не будем здесь касаться определения площади произвольной криволинейной фигуры. Скажем лишь, что в тех случаях, когда эта площадь определена, она равна пределу площадей некоторой последовательности многоугольников, вписанных в рассматриваемую фигуру. Из теории пределов известно следующее предположение: если последовательность \(S_{n}\) стремится к пределу \(S\), то последовательность \(\delta S_{n}\), где \(\delta\) постоянное, стремится к пределу \(\delta S\). На основании этого предложения мы заключаем, что формула \eqref{ref5} справедлива в самом общем случае.

В качестве примера найдем выражение площади эллипса через его полуоси. Ранее мы , что эллипс с полуосями \(a\) и \(b\) может быть получен сжатием окружности радиуса \(a\) к прямой, проходящей через ее центр. Коэффициент сжатия равен \(b/a\). В одном из мы получили координатную запись сжатия к прямой \(x^{*}=x\), \(y^{*}=\lambda y\). Детерминант из коэффициентов в этих формулах равен \(\lambda\), то есть в нашем случае \(b/a\). Таким образом, отношение площади эллипса к площади окружности равно \(b/a\), и эта площадь равна \(S=(b/a)\pi a^{2}\). Окончательно имеем
$$
S=\pi ab.\nonumber
$$

Образы линий второго порядка.

Мы видели, что прямая линия переходит в прямую. Это частный случай следующего утверждения.

Утверждение 3.

Аффинное преобразование переводит алгебраическую линию в алгебраическую линию того же порядка.

Доказательство.

В самом деле, пусть линия \(L\) в декартовой системе координат \(O, \boldsymbol{e}_{1}, \boldsymbol{e}_{2}\) имеет алгебраическое уравнение порядка \(p\). Мы уже , что образы всех точек линии \(L\) при аффинном преобразовании \(f\) имеют в системе координат \(f(O), f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2})\) те же координаты, что и их прообразы в системе координат \(O, \boldsymbol{e}_{1}, \boldsymbol{e}_{2}\). Следовательно, координаты образов в системе \(f(O), f(\boldsymbol{e}_{1}), f(\boldsymbol{e}_{2})\) связаны тем же алгебраическим уравнением порядка \(p\). Этого достаточно, чтобы сделать нужное нам заключение.

Из доказанного выше утверждения, в частности, следует, что линия второго порядка при аффинном преобразовании перейдет в линию второго порядка. Мы докажем более сильное утверждение. Как мы уже знаем, линии второго порядка можно разделить на . Мы увидим, что класс линии сохраняется при аффинном преобразовании. На этом основании классы линий, перечисленные в указанной теореме, называются аффинными классами. Итак, докажем новое утверждение.

Утверждение 4.

Линия второго порядка, принадлежащая к одному из аффинных классов, при любом аффинном преобразовании может перейти только в линию того же класса. Каждую линию второго порядка подходящим аффинным преобразованием можно перевести в любую другую линию того же аффинного класса.

Доказательство.

Линию мы назовем ограниченной, если она лежит внутри некоторого параллелограмма. Легко видеть, что при аффинном преобразовании ограниченная линия должна перейти в ограниченную, а неограниченная - в неограниченную.

1. Эллипс - ограниченная линия второго порядка. Кроме эллипсов ограничены только линии, состоящие из одной точки, то есть пары мнимых пересекающихся прямых. Поскольку эллипс ограничен и состоит больше, чем из одной точки, он может перейти только в эллипс.
2. Гипербола состоит из двух отдельных ветвей. Это свойство можно сформулировать так, что будет ясна его неизменность при аффинных преобразованиях. Именно, существует прямая линия, не пересекающая гиперболу, но пересекающая некоторые ее хорды.Из всех линий второго порядка только гиперболы и пары параллельных прямых обладают этим свойством. У гиперболы ветви не прямые линии, и потому при аффинном преобразовании она может перейти только в гиперболу.
3. Парабола - неограниченная линия второго порядка, состоящая из одного непрямолинейного куска. Этим свойством не обладают никакие другие линии второго порядка, и потому парабола может перейти только в параболу.
4. Если линия второго порядка представляет собой точку (пару мнимых пересекающихся прямых), прямую (пару совпавших прямых), пару пересекающихся или пару параллельных прямых, то из доказанных ранее свойств аффинных преобразований следует, что эта линия не может перейти в линию никакого другого класса.

Докажем вторую часть предложения. В уже доказанной нами канонические уравнения линий второго порядка написаны в декартовой прямоугольной системе координат и содержат параметры \(a, b, …\) Если мы откажемся от ортонормированности базиса, то сможем произвести дальнейшие упрощения канонических уравнений и привести их к виду, не содержащему параметров. Например, замена координат \(x’=x/a\), \(y’=y/b\) переводит уравнение эллипса \(x^{2}a^{2}+y^{2}b^{2}=1\) в уравнение \(x’^{2}+y’^{2}=1\), каковы бы ни были \(a\) и \(b\). (Последнее уравнение не есть уравнение окружности, так как новая система координат не декартова прямоугольная.)

Читатель без труда покажет, что канонические уравнения линий второго порядка переходом к подходящей системе координат могут быть преобразованы в уравнения:

1. \(x^{2}+y^{2}=1\);
2. \(x^{2}+y^{2}=0\);
3. \(x^{2}-y^{2}=1\);
4. \(x^{2}-y^{2}=0\);
5. \(y^{2}=2x\);
6. \(y^{2}-1=0\);
7. \(y^{2}=0\).

Такую систему координат мы назовем аффинной канонической системой координат.

Из ранее следует, что аффинное преобразование, которое совмещает аффинные канонические системы координат двух линий одного аффинного класса, совмещает и эти линии. Это заканчивает доказательство.

Разложение ортогонального преобразования.

Теорема 1.

Каждое ортогональное преобразование раскладывается в произведение параллельного переноса, поворота и, возможно, осевой симметрии.

Доказательство.

Пусть \(f\) - ортогональное преобразование и \(\vartriangle ABC\) - равнобедренный прямоугольный треугольник с прямым углом \(A\). При преобразовании \(f\) он перейдет в равный ему треугольник \(\vartriangle A^{*}B^{*}C^{*}\) с прямым углом при вершине \(A^{*}\). Теорема будет доказана, если, производя последовательно параллельный перенос \(p\), поворот \(q\) и (в случае необходимости) осевую симметрию \(r\), мы сможем совместить треугольники \(ABC\) и \(A^{*}B^{*}C^{*}\). Действительно, произведение \(rqp\) - аффинное преобразование так же, как и \(f\), а аффинное преобразование однозначно определяется образами трех точек, не лежащих на одной прямой. Поэтому \(rqp\) совпадает с \(f\).

Итак, переведем \(A\) и \(A^{*}\) параллельным переносом \(p\) на вектор \(\overrightarrow{AA^{*}}\) (если \(A=A^{*}\), то \(p\) - тождественное преобразование). Затем поворотом \(q\) вокруг точки \(A^{*}\) совместим \(p(B)\) с \(B^{*}\) (возможно, и это преобразование окажется тождественным). Точка \(q(p(C))\) либо совпадает с \(C^{*}\), либо симметрична ей относительно прямой \(A^{*}B^{*}\). В первом случае цель уже достигнута, а во втором потребуется осевая симметрия относительно указанной прямой. Теорема доказана.

Следует иметь в виду, что полученное разложение ортогонального преобразования не однозначно. Более того, можно поворот или параллельный перенос разложить в произведение осевых симметрий, произведение параллельного переноса и поворота представить как один поворот и так далее. Мы не будем уточнять, как это сделать, а выясним следующее общее свойство всех таких разложений.

Утверждение 5.

При любом разложении ортогонального преобразования в произведение любого числа параллельных переносов, поворотов и осевых симметрий четность числа осевых симметрий, входящих в разложение, одна и та же.

Доказательство.

Для доказательства рассмотрим на плоскости произвольный базис и проследим за изменением его ориентации (направления кратчайшего поворота от \(\boldsymbol{e}_{1}\) к \(\boldsymbol{e}_{2}\)) при осуществляемых преобразованиях. Заметим, что поворот и параллельный перенос не меняют ориентацию ни одного базиса, а осевая симметрия меняет ориентацию любого базиса. Поэтому, если данное ортогональное преобразование меняет ориентацию базиса, то в любое его разложение должно входить нечетное число осевых симметрий. Если же ориентация базиса не меняется, то число осевых симметрий, входящих в разложение, может быть только четным.

Определение.

Ортогональные преобразования, которые могут быть разложены в произведение параллельного переноса и поворота, называются ортогональными преобразованиями первого рода , а остальные - ортогональными преобразованиями второго рода .

Ортогональное преобразование в декартовой прямоугольной системе координат записывается :
$$
\begin{array}{cc}


\end{array}.\nonumber
$$
При верхних знаках коэффициентов у \(y\) в этих формулах детерминант, составленный из коэффициентов, равен +1, а при нижних знаках он равен -1. Отсюда и из формулы \eqref{ref4} следует следующее утверждение.

Утверждение 6.

Ортогональное преобразование первого рода записывается в декартовой прямоугольной системе координат формулами
$$
\begin{array}{cc}
& x^{*}=x \cos \varphi \mp y \sin \varphi+c_{1},\\
& y^{*}=x \sin \varphi \pm y \cos \varphi+c_{2}.
\end{array}.\nonumber
$$
с верхними знаками у коэффициентов при \(y\), а ортогональное преобразование второго рода - с нижними знаками.

Разложение аффинного преобразования.

Мы видели, насколько аффинное преобразование может изменить плоскость: окружность может перейти в эллипс, правильный треугольник - в совершенно произвольный. Казалось бы, никакие углы при этом сохраниться не могут. Однако имеет место следующее утверждение

Утверждение 7.

Для каждого аффинного преобразования существуют две взаимно перпендикулярные прямые, которые переходят во взаимно перпендикулярные прямые.

Доказательство.

Для доказательства рассмотрим какую-либо окружность. При данном аффинном преобразовании она перейдет в эллипс. Каждая ось эллипса - множество середин хорд, параллельных другой оси. При аффинном преобразовании хорда перейдет в хорду, параллельность должна сохраниться, а середина отрезка переходит в середину его образа. Поэтому прообразы осей эллипса - отрезки, обладающие тем же свойством: каждый из них есть множество середин хорд окружности, параллельных другому отрезку. Такие отрезки непременно являются двумя взаимно перпендикулярными диаметрами окружности. Это то, что нам требовалось: существуют два взаимно перпендикулярных диаметра окружности, которые переходят во взаимно перпендикулярные отрезки - оси эллипса.

Стоит отметить один особый случай: окружность при аффинном преобразовании может перейти в окружность. В этом случае то же рассуждение проходит с любыми двумя взаимно перпендикулярными диаметрами окружности-образа. Очевидно, что при этом любые два взаимно перпендикулярных направления остаются перпендикулярными.

Определение.

Два взаимно перпендикулярных направления называются главными или синугулярными направлениями аффинного преобразования \(f\), если они переходят во взаимно перпендикулярные направления.

Теорема 2.

Каждое аффинное преобразование раскладывается в произведение ортогонального преобразования и двух сжатий к двум взаимно перпендикулярным прямым.

Доказательство.

Доказательство аналогично доказательству . Рассмотрим аффинное преобразование \(f\) и выберем равнобедренный прямоугольный треугольник \(ABC\) так, чтобы его катеты \(AB\) и \(AC\) были направлены вдоль главных направлений преобразования \(f\). Обозначим через \(A^{*}\), \(B^{*}\) и \(C^{*}\) образы его вершин. Сделаем такое ортогональное преобразование \(g\), при котором \(g(A)=A^{*}\), а точки \(g(B)\) и \(g(C)\) лежат соответственно на лучах \(A^{*}B^{*}\) и \(A^{*}C^{*}\). (Этого легко добиться, как и в теореме 1, параллельным переносом, поворотом и осевой симметрией.)

Пусть \(\lambda=|A^{*}B^{*}|/|A^{*}g(B)|\), a \(\mu=|A^{*}C^{*}|/|A^{*}g(C)|\). Тогда сжатие \(p_{1}\) к прямой \(A^{*}C^{*}\) в отношении \(\lambda\) переведет \(g(B)\) в \(p_{1}g(B)=B^{*}\) и не сдвинет точек \(A^{*}\) и \(g(C)\). Аналогично, сжатие \(p_{2}\) к прямой \(A^{*}B^{*}\) переведет \(g(C)\) в \(p_{2}g(C)=C^{*}\) и не сдвинет точек прямой \(A^{*}B^{*}\).

Это означает, что произведение \(p_{2}p_{1}g\) переводит точки \(A\), \(B\) и \(C\) в точки \(A^{*}\), \(B^{*}\) и \(C^{*}\) так же, как и заданное нам преобразование \(f\). Согласно ранее доказанному имеем \(p_{2}p_{1}g=f\), как и требовалось.